VectorSphericalWaveFunction¶
| Type: | section |
|---|---|
| Appearance: | multiple |
Specifies an illuminating, time-harmonic vector spherical wave function,
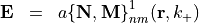
To specify a vector spherical wave function illumination the following parameters are required:
- the scaling Coefficient
 ,
, - the angular frequency Omega or vacuum wavelength Lambda0,
- the integer multipole degree
n, ordermand type (N or M) of the vector spherical wave function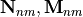 ,
,
SourceBag {
Source {
ElectricFieldStrength {
VectorSphericalWaveFunction {
Coefficient = 1
Lambda0 = 50e-9
MultipoleDegree = 1
MultipoleOrder = -1
Type = M
}
}
}
}
Theoretical background
It is required that the exterior of the computational domain is a lossless, homogeneous and isotropic material distribution enclosing the origin of the vector spherical wave function. Let 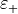 and
and 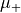 denote the corresponding scalar permittivity and permeability, respectively. The angular wave number is given by
denote the corresponding scalar permittivity and permeability, respectively. The angular wave number is given by 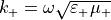 .
.
The vector spherical wave functions 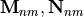 for the incoming fields have the following definition [1] in terms of spherical coordinates
for the incoming fields have the following definition [1] in terms of spherical coordinates 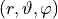
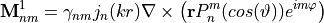
![\begin{eqnarray*}
\pvec{N}^{1}_{nm} = \frac{1}{k} \nabla \times \pvec{M}^{1}_{nm} = \gamma_{nm} \left[ \frac{n(n+1)}{kr}j_{n}(kr) \frac{\pvec{r}}{r} P_{n}^m(cos(\vartheta))e^{im\varphi} + \frac{r}{kr} \frac{d}{d(kr)}\left(kr j_n(kr)\right) \nabla \left( P_{n}^m(cos(\vartheta))e^{im\varphi} \right) \right]
\end{eqnarray*}](_images/math/2513a678d08f859b7a42f7d224bcfadd129203a2.png)
with the common normalization factor
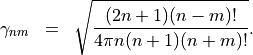
The definition makes use of the spherical Bessel functions 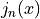 and the associated Legendre polynomials
and the associated Legendre polynomials 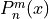 of
degree
of
degree 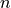 and order
and order 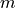
Bibliography
| [1] | Mishchenko, Michael I., Larry D. Travis, and Andrew A. Lacis. Scattering, absorption, and emission of light by small particles. Cambridge university press, 2002. |