Optimization¶
In this section we present a way to efficiently optimize an optical structure. The optimization algorithm is based on a Bayesian optimization approach [Schn2017], which requires substantially fewer simulation results than other optimization algorithms [Schn2019]. As an example we revisit the structure with a square unit cell discussed in the EM-tutorial. The goal of the optimization is to create a silicon metasurface with a minimal reflectivity, which can act as an antireflective coating. The design and fabrication of such a coating has been discussed in [Prou2016].
We consider a periodic grating with square-like structures. The variable parameters of the system are shown in the figure below.
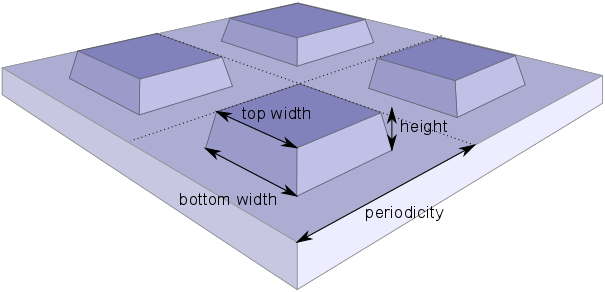
The metasurface is parametrized by the periodicity, the height of the etched structures, their bottom, and their top widths.¶
First, we define the search domain for the minimization of the reflectivity:
domain = [
{'name': 'height', 'type': 'continuous', 'domain': (50,200)},
{'name': 'top_width', 'type': 'continuous', 'domain': (60,200)},
{'name': 'bottom_width', 'type': 'continuous', 'domain': (60,200)},
{'name': 'periodicity', 'type': 'continuous', 'domain': (150,400)}
]
The bottom and top widths may not exceed the periodicity of the structure. Hence, we have to define two constraints of the search domain. A constraint is defined by a function expression that returns a negative value, if and only if the constraint is fulfilled.
constraints = [
{'name':'max_bottom_width', 'constraint': 'bottom_width - periodicity + 10'},
{'name':'max_top_width', 'constraint': 'top_width - periodicity + 10'}
]
With the domain and constraints variables one can now create a new study object. We set the maximal number of optimization iterations to 20 and the number of parallel evaluations of the objective function to 2.
study = jcmwave.optimizer.create_study(domain=domain, constraints=constraints,
name='Optimization of antireflection coating')
study.set_parameters(max_iter=20, num_parallel=2)
In order to perform parallel evaluations of the objective function, we start up the daemon. Details on how to use the daemon are described in the tutorial Parallel Parameter Scan.
jcmwave.daemon.startup()
jcmwave.daemon.add_workstation(
Hostname='localhost',
Multiplicity=2, NThreads=1)
Next, we define the objective function, that computes the reflectivity of the metasurface based on the Fourier coefficients in Z direction [*]. The convergence of the optimization can be largely improved by providing also derivative information. To this end the derivatives of the Fourier coefficients are calculated by the solver as described in this tutorial example . The objective function returns an observation object containing the objective value and its derivatives.
def objective(**kwargs):
keys = kwargs
keys['slc'] = 150
# The reflectivity is averaged over the wavelengths 600nm 700nm 800nm
lambdas = [600, 700, 800]
permittivities = [15.590 + 0.21635j, 14.317 + 0.092101j, 13.646 + 0.048345j]
# Do a parallel lambda-scan
job_ids = []
for idx, lambda0 in enumerate(lambdas):
keys['lambda0'] = lambda0*1e-9
keys['permittivity'] = permittivities[idx]
job_id = jcmwave.solve('project.jcmp', keys,
temporary=True)
job_ids.append(job_id)
results, logs = jcmwave.daemon.wait(job_ids)
# Sum up reflectivities and their parameter derivatives for each wavelength
reflectivity = 0
derivatives = np.zeros(len(domain))
for idx, lambda0 in enumerate(lambdas):
# The Fourier coefficients are stored in the results of the first post process
FC = results[idx][1]['ElectricFieldStrength'][0]
# Reflectivity for the current wavelength
this_reflectivity = np.sum(np.real(FC)**2 + np.imag(FC)**2)
# Averaged reflectivity
reflectivity += this_reflectivity/len(lambdas)
for idx2,info in enumerate(domain):
# Get derivatives of Fourier coefficients from the entries 'd_height', 'd_top_width', ...
dFC = results[idx][1]['d_'+info['name']]['ElectricFieldStrength'][0]
# Derivatives of the reflectivity according to the chain rule
d_this_reflectivity = np.sum(2*(np.real(FC)*np.real(dFC) +
np.imag(FC)*np.imag(dFC)))
derivatives[idx2] += d_this_reflectivity/len(lambdas)
# Create a new observation object and add the objective value
# and its derivatives
observation = study.new_observation()
observation.add(reflectivity)
for idx,info in enumerate(domain):
observation.add(derivative=info['name'], value=derivatives[idx])
return observation
Finally, we run the minimization. To this end we retrieve new parameter values by calling suggestion=study.get_suggestion(). For each suggestion the corresponding observation returned by the objective function is added to the study by calling study.add_observation(observation, suggestion.id). In order to calculate multiple objective functions in parallel, we start them in separate threads.
def acquire(suggestion):
observation = objective(**suggestion.kwargs)
study.add_observation(observation, suggestion.id)
# Run the minimization
while (not study.is_done()):
suggestion = study.get_suggestion()
t = threading.Thread(target=acquire, args=(suggestion,))
t.daemon = True
t.start()
The same thread-based acquisition cycle is also performed by calling:
study.set_objective(objective)
study.run()
The progress of the optimization can be examined in a dashboard, that is shown in a browser window. A typical example is shown in the figure below. By optimizing the parameters one can reduce the reflectivity from 30% to below 1%.
Input Files
| [*] | To speed up the computation times for this tutorial example, we set the side length constraint of the mesh to 150nm (keys['slc']=150). In order to obtain converged results, one should rather use a value of 40nm. |
| [Schn2019] | P.-I. Schneider, X. Garcia Santiago, V. Soltwisch, M. Hammerschmidt, S. Burger, C. Rockstuhl. Benchmarking Five Global Optimization Approaches for Nano-optical Shape Optimization and Parameter Reconstruction ACS Photonics 6, 2726 (2019) https://doi.org/10.1021/acsphotonics.9b00706 https://arxiv.org/abs/1809.06674 |
| [Schn2017] | P.-I. Schneider, X. Garcia Santiago, C. Rockstuhl, S. Burger. Global optimization of complex optical structures using Bayesian optimization based on Gaussian processes Proc. SPIE 10335 (2017) 103350O (2017) https://doi.org/10.1117/12.2270609 https://arxiv.org/abs/1707.08479 |
| [Prou2016] | Julien Proust, Anne-Laure Fehrembach, Frédéric Bedu, Igor Ozerov and Nicolas Bonod. Optimized 2D array of thin silicon pillars for efficient antireflective coatings in the visible spectrum. Scientific Reports volume 6, Article number: 24947 (2016) http://dx.doi.org/10.1038/srep24947 |
