ScatteringMatrix¶
This post process computes a number of quantities used in ellipsometry and scatterometry from the far field of a simulation. As an input it needs the result from the FourierTransform post process, whose results have to be aligned, such that the z-Axis is the optical axis. This can be achieved by corresponding simulation setup or a CoordinateRenaming in the FourierTransform post process. Further, the sources of the initial project have to be plane waves, and for each incidence direction two non-parallel polarizations have to be defined.
The basis of this post process is the SP-Jones matrix. It defines how the amplitude of an S- or P-polarized incidence wave is scattered or transmitted into the S- and P-direction, defined by the outgoing direction.
There is a large number of different possibilities how to define S- and P-direction. Each physical or engineering community basically has its own. You may use PolarizationConvention to switch to your prefered one.
In JCMsuite the convention described in PlaneWave is used by default. The key properties of this definition are the following:
If a wave propagates in +Z or -Z direction, the S-direction is aligned along +Y and the P-direction along +X. The X- and Y-axis are rotated to give the S- and P-direction according to 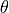 and
and 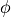 of the incidence or outgoing direction. Thereby,
of the incidence or outgoing direction. Thereby, 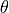 is always the angle between the Z-axis and the propagation direction. It is restricted between 0 and 90 degrees. Definition of angle
is always the angle between the Z-axis and the propagation direction. It is restricted between 0 and 90 degrees. Definition of angle 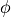 for upward or downward propagating fields can best be understood from the drawing given in PlaneWave.
for upward or downward propagating fields can best be understood from the drawing given in PlaneWave.
A number of quantities derived from the Jones matrix are further computed and written into the output table. These are:
- 4x4 Mueller matrix
- Rho:

- Delta and Psi defined by:
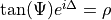
Further, all the quantities are defined for SP-directions and Sigma/XY-directions as defined in PlaneWave.
The incoming and outgoing directions of the computed quantities are given by their corresponding incidence and outgoing k-Vectors and 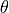 and
and 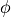 .
.