Static¶
| Type: | section |
|---|---|
| Appearance: | simple |
This section defines a project to compute the stationary deformation of a body, when exposed to prescribed loading conditions such as external forces or initial stresses. The major aim is to compute the arising internal stresses.
In the following, 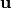 denotes the displacement field. The original body filling the reference domain
denotes the displacement field. The original body filling the reference domain  is deformed to a body
is deformed to a body  The deformed body is related to the reference body by the deformation mapping
The deformed body is related to the reference body by the deformation mapping  ,
,

and one defines the component-wise deformation gradient 
![\begin{eqnarray*}
\nabla \VField{\phi} & = & \left [
\begin{array}{ccc}
\partial_x \phi_x & \partial_y \phi_x & \partial_z \phi_x \\
\partial_x \phi_y & \partial_y \phi_y & \partial_z \phi_y \\
\partial_x \phi_z & \partial_y \phi_z & \partial_z \phi_z \\
\end{array}
\right ] \equiv \partial_j \phi_i
\end{eqnarray*}](_images/math/f66ea566728ef72b0bf2a9313272ec56aa2db20b.png)
A non-constant deformation field gives rise to a local change of the metric (compared to the reference body) which is given by the Cauchy-Green deformation tensor,

The derivation from the original Euclidean metric is called strain and is quantified by the Green-Lagrangian strain tensor

which is expressed in terms of the displacement field 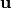 . Within the linear theory the second, quadratic term is neglected and the so gained linear strain is denoted by
. Within the linear theory the second, quadratic term is neglected and the so gained linear strain is denoted by  ,
,

Warning
A linear model is used. It is only valid for sufficiently small displacements.
Within the linear theory the constitutive relation between the stress and the (linear strain) reads as

where 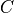 is the stiffness tensor and
is the stiffness tensor and  is the prescribed initial strain.
is the prescribed initial strain.
The equations governing linear elasticity follow from the minimum principle for the elastic energy:

This condition is supplemented by boundary conditions, c.f., boundary condition section ContinuumMechanics.
Plane strain problems
Prismatic structures, such as an optical fiber, with a  -dimension much larger than the cross-section diameter are treated by the plane strain assumption: It is assumed that the strain tensor is independent of the
-dimension much larger than the cross-section diameter are treated by the plane strain assumption: It is assumed that the strain tensor is independent of the  -coordinate and that all entries of the strain tensor involving a
-coordinate and that all entries of the strain tensor involving a  -direction are zero, that is,
-direction are zero, that is,  . In this case a two dimensional grid file has to be passed to
. In this case a two dimensional grid file has to be passed to JCMsolve.
Implicitly defined quantities
The table below lists field quantities which are implicitly defined within the solution fieldbag. This way they can be used by subsequent post-processes.
| Quantity | Expression | JCM Tag |
|---|---|---|
| Strain |  |
Strain |
| Stress |  |
Stress |
Bibliography
| [1] | Braess D., Finite elements: theory, fast solvers, and applications in solid mechanics, Cambridge University Press, 2001. |
| [2] | Okamoto K., Fundamentals of Optical Waveguides, Academic Press, 2006. |