BlochFamily¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | PropagatingModes |
The BlochFamily multiple source allows a comfortable definition of all incident plane waves sharing the same Bloch phase in periodic geometries. As discussed here, periodic structures support a set of discrete diffraction orders, or Fourier modes that are linked to the reciprocal grid in k space. This source definition sets up plane wave illuminations incident from all these discrete directions separately for s and p polarization. A table containing the K and Amplitude vector of the different illumination is exported if the OutputFileName is provided.
MultipleSources {
BlochFamily {
Lambda0 = 800e-9
Sigma = [0 0]
Incidence = Both
OutputFileName = "sourceTable.jcm"
}
In the following we focus on the two-fold periodic case only.
From the grid the two lattice vectors  and
and  with their respective reciprocal grid vectors
with their respective reciprocal grid vectors  ,
,  are determined automatically. The same holds for
are determined automatically. The same holds for  and
and  , the corresponding scalar permittivities and permeabilities in the lower and upper half spaces, respectively. The angular wave number is given by
, the corresponding scalar permittivities and permeabilities in the lower and upper half spaces, respectively. The angular wave number is given by  .
.
Using reciprocal grid vectors the transversal components  of the k-vector is determined for given integers
of the k-vector is determined for given integers  . By prescribing the transversal component of the Bloch vector
. By prescribing the transversal component of the Bloch vector 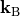 (this can set using Sigma), the illuminations can be translated in reciprocal space.
This remaining normal component
(this can set using Sigma), the illuminations can be translated in reciprocal space.
This remaining normal component  is determined by
is determined by  in the appropriate half spaces.
in the appropriate half spaces.