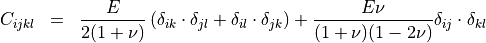Stiffness¶
| Type: | 4-Tensor, or section |
|---|---|
| Range: | [v_1, …, v_81] |
| Default: | -/- |
| Appearance: | optional |
Defines stiffness tensor  also called elasticity tensor. Units are pascals,
also called elasticity tensor. Units are pascals, 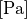 , which corresponds to force per unit area.
, which corresponds to force per unit area.
This stiffness tensor relates the strain  of a body to the stresses within the body. In the used linear form this relation is given by:
of a body to the stresses within the body. In the used linear form this relation is given by:
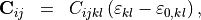
where 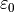 is the initial strain of the body, i.e., the strain for which the body is free of stresses.
is the initial strain of the body, i.e., the strain for which the body is free of stresses.
When the Poisson ratio  (see PoissonRatio) and the Young modulus
(see PoissonRatio) and the Young modulus 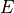 (see YoungModulus) are set, a stiffness tensor is implicitly defined by the following expression when not otherwise specified:
(see YoungModulus) are set, a stiffness tensor is implicitly defined by the following expression when not otherwise specified: