Data Structure¶
All .jcm input files share a common data structure representing a data tree. A data tree consists of nested sections containing key-value lists of primitive parameters. See below for a list of the available primitives.
In the text based .jcm input files a section is represented by a tag (=name) followed by an opening bracket ‘{‘. A section is closed by a closing bracket ‘}’, after declaring primitive parameters and nested subsections.
Note
The following examples are useful to explain the data structure of the .jcm files. At this position it is not necessary to understand what the syntax in the examples means in greater detail.
Example 1:
The material file materials.jcm may contain a section like this:
Material {
DomainId = 5
RelPermeability = 1.0
RelPermittivity = 2.25
}
Here, Material is a section tag. DomainId, RelPermeability and RelPermittivity denote primitive parameters. This section defines an isotropic relative permittivity and an isotropic relative permeability for the domain with id ‘5’.
It should also be possible to define a relative permittivity which is anisotropic and which exhibits a stress-induced birefringence. A declaration of such a material may look like this:
Example 2:
Material {
DomainId = 5
RelPermeability = 1.0
RelPermittivity {
Constant = [2.25 0.00 0.00
0.00 2.24 0.00
0.00 0.00 2.24]
PhotoElasticCorrection {
...
}
}
}
The section PhotoElasticCorrection contains further definitions to set the photo-elastic properties of the material.
In this example the tag RelPermittivity has now the meaning of a section. The example has three nested sections, Material, RelPermittivity and PhotoElasticCorrection, and shows how input data can be defined in a more complex way.
Each .jcm input file comes with a schema specifying which section and primitive tags are allowed. The schema also defines the value types of the primitive parameters and declares default values. In other words, a valid input must match the underlying schema. For more information see chapter Input Schema.
Once the type of a primitive is known it must be given in an appropriate form.
The following table lists all primitive types, gives a short explanation and shows the corresponding formats:
| primitive type | description | format | examples |
|---|---|---|---|
| int | integer number | standard integer number | 3 |
| float | real number | standard floating point number | 2.1108, 5e9 |
| complex | complex number | Matlab, Python, or C++ style | 2.1+1.1i, 2.1+1.1j, (2.1, 1.1) |
| enum | enumeration | non-quoted string from list given by the schema | ASCII |
| boolean | yes or no |
yes |
|
| string | doubly quoted string | “GaAs” | |
| file | path to a file or directory | doubly quoted string, use Unix separators ‘/’, relative paths refers to file of definition | “./project_results/fieldbag.jcm”
“C:/Programs and Files/JCM”
|
| vector<int> | integer vector | Matlab like, size specified by the schema | [11 12] |
| vector<float> | float vector | see above | [0:0.5:2.5] |
| vector<complex> | complex vector | see above | [1 1+0.5i] |
| matrix<int> | integer matrix | Matlab like, size specified by the schema | [1 0; 0 1] |
| matrix<float> | float matrix | see above | |
| matrix<complex> | complex matrix | see above | |
| 0-Tensor | rank 0 tensor (scalar) | as complex, putting into
[] brackets allowed |
3.1 |
| 1-Tensor | rank 1 tensor | complex 3-vector | [3.1, 2, 0] |
| 2-Tensor | rank 2 tensor | complex (3 by 3)-matrix
complex scalar
(gives isotropic tensor)
3-vector
(gives diagonal tensor)
|
[1.0 0.1 0.0
0.1 1.0 0.0
0.0 0.0 1.0]
|
| 4-Tensor | rank 4 tensor | vector of size 81 | [3, …, 6] |
| Rotation | rotation matrix | real 3 by 3 rotation,
coordinate renaming tag,
2 unit directions
(3 by 2 matrix ),
Euler angles
(1 by 3 vector)
(see comment) |
X:Z:-Y
[90, 30, 0]
|
Comments:
Coordinate Renaming
A coordinate renaming is a special kind of a rotation matrix which interchanges the Cartesian coordinates without changing the orientation. A coordinate renaming may be given as a tag of the form “<AX>:<AY>:<AZ>”, where <AX>, <AY> and <AZ> are the new labels (“X”, “Y”, “Z”, “-X”, “-Y”, or “-Z”) of the original Cartesian axis. For example X:Z:-Y gives the following rotation matrix:
![\begin{eqnarray*}
R & = &
\left [
\begin{array}{rrr}
1.0 & 0.0 & 0.0 \\
0.0 & 0.0 & -1.0 \\
0.0 & 1.0 & 0.0 \\
\end{array}
\right ]
\end{eqnarray*}](_images/math/621c10043cbf5a03e12627bbd6c67ec86b1f9151.png)
Two directions definition
- The two directions are interpreted as the columns of a 3 by 2 matrix. A right handed coordinate system is constructed such that
- The Z-axis is rotated onto the first vector.
- The X-axis is rotated onto the second vector.
Both vectors are normalized first.
Euler angles
There are different conventions of defining rotations with Euler angles. Here, we employ the
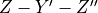 convention which rotates first around the Z-axis by the angle
convention which rotates first around the Z-axis by the angle 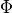 , then around the Y’-axis (the Y-axis in the rotated frame) by
, then around the Y’-axis (the Y-axis in the rotated frame) by 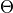 and lastly around the
and lastly around the 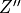 axis (Z-axis of the twice rotated frame) by
axis (Z-axis of the twice rotated frame) by 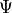 . The rotation matrix R is thus computed as
. The rotation matrix R is thus computed as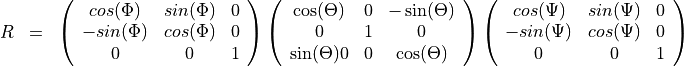
The angles are entered as a vector
![[\Phi, \, \Theta, \, \Psi]](_images/math/1752882dafb2446d8fd76242d352cc7f0a5fada8.png) where the angles are given in degrees. Entry of a short vector
where the angles are given in degrees. Entry of a short vector 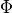 or
or ![[\Phi, \, \Theta]](_images/math/cb4bf7bc63e91ca66ce31fdb75b638a37e744660.png) is allowed. In these cases
is allowed. In these cases  or
or  is implicetely assumed.
is implicetely assumed.