ObjectSidedJonesExpansion¶

Type:	Matrix<float>
Range:	[v_11, …, v_1j; …; v_i1, …; v_ij], j<=4
Default:	-/-
Appearance:	optional

This vector parameter is used to define the object-sided Jones aberration function 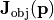$\TField{J}_\mathrm{obj}(\pvec{p})$ as introduced in the parent section OpticalSystem. This is done by means of an expansion into Zernike polynomials.

Note

The 2-by-2 Jones matrix acts on the 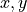$x, y$ components of the electric field in the pupil plane.

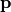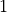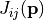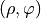As the amplitude of the normalized coordinate vector $\pvec{p}$ ranges from $0$ to $1$ , components of the Jones matrix $J_{ij}(\pvec{p})$ are defined on the unit disk and one may switch to polar coordinates $(\rho, \varphi)$ ,

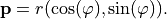
$\begin{eqnarray*} \pvec{p} = r (\cos(\varphi), \sin(\varphi)). \end{eqnarray*}$

The Jones aberration matrix 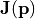$\TField{J}(\pvec{p})$ is expanded into Zernike polynomials,

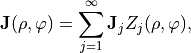
$\begin{eqnarray*} \TField{J}(\rho, \varphi) = \sum_{j=1}^{\infty} \TField{J}_j Z_j(\rho, \varphi), \end{eqnarray*}$

where 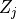$Z_j$ are the Zernike polynomials and 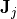$\TField{J}_j$ are the 2-by-2 matrix expansion coefficients as passed by the discussed vector parameter. Hereby, four subsequent entries of the parameter vector form a matrix 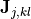$\TField{J}_{j, kl}$ . E.g. the input may look like this:

JonesExpansion = [ J1_11 J1_12
                   J1_21 J2_22

                   J2_11 J2_12
                   J2_21 J2_22

                   ...
                 ]

Warning

Different orderings and different scalings of the Zernike polynomials are in use. The section Zernike Polynomials in the appendix gives a detailed definition of the Zernike polynomials as used in JCMsuite.

Section ZernikeCoefficient allows for an alternative definition of a Jones pupil coefficient. There, the index pair 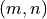$(m, n)$ can be used.