Python¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | OutputQuantity |
This section is used to define a flux density expression by means of a Python script. JCMsuite comes with a Python interpreter, therefore an installation of Python is not required.
Note
Since Version 6.2.0 JCMsuite uses Python 3.10 as available from http://www.python.org. It further includes the NumPy-package, see http://www.scipy.org.
The Python script based integrand definition is very flexible and general, since it is possible to define parameter-dependent expressions. These parameters may not only contain user-defined fixed values, but may also describe dependencies on tensor fields. Furthermore, it offers a simple way to compute mutual overlap integrals.
To explain this in more detail, let us denote the flux density - tensor field we want to define by
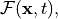 where
where 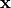 is the position vector and
is the position vector and 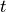 is the time. The flux density - tensor field which may depend on the values of other tensor fields
is the time. The flux density - tensor field which may depend on the values of other tensor fields 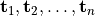 at the same position
at the same position 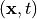 is described as:
is described as:
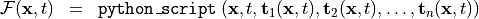
The Python script 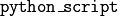 is provided by the user. There are two options to do this:
is provided by the user. There are two options to do this:
- Inline definition of a python expression directly within the post-process file, see section Expression.
- Reference to a function contained in a python module, see section Function.
The argument values 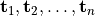 as well as the positions
as well as the positions 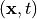 should be passed from
should be passed from JCMsolve to the python script when evaluating the flux density field. For being able to do this, the user has to inform JCMsolve which parameters are actually needed. In the words of a computer programming language the user has to specify the signature of the python script. This is done by filling the Parameter section.
JCMsolve computes the integral values for each physical domain 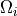 separately (
separately (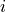 is the domain index):
is the domain index):

A tensor field parameter is ambiguous when imported from a JCM fieldbag which contains more than one field of the desired type. In this case, JCMsolve should compute the integral values for each field separately. This necessitates an additional integral index.
More generally, we allow for more than one integral indices to compute mutual overlap integrals. For each tensor field parameter  one specifies which integral index runs with the field index:
one specifies which integral index runs with the field index:

Here, the super indices 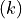 and
and 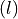 denote the field index of the tensor field parameters. In the above, the field index of the first tensor field parameter
denote the field index of the tensor field parameters. In the above, the field index of the first tensor field parameter  runs with the first integral index
runs with the first integral index 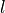 , whereas the field index of
, whereas the field index of 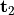 runs with the second index
runs with the second index 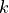 .
.