Electromagnetics¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | ContinuumMechanics, HeatConduction |
Electromagnetic field problems address the computation of the electromagnetic field. This means the following impressed tensor fields are computed: the electric field strength 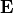 , the electric flux density
, the electric flux density 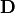 ,
the magnetic field strength
,
the magnetic field strength  ,
and the magnetic flux density
,
and the magnetic flux density  .
.
Macroscopically, these fields are related by Maxwell’s equations

where 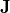 and
and  are the macroscopically free current and charge distributions, respectively. Maxwell’s equations are supplemented by constitutive relations characterizing the macroscopic medium.
are the macroscopically free current and charge distributions, respectively. Maxwell’s equations are supplemented by constitutive relations characterizing the macroscopic medium. JCMsolve supports dispersive and anisotropic materials given by a linear relation in the frequency domain:

Here,  and
and 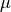 are the permittivity and the permeability tensors, respectively. The tensors
are the permittivity and the permeability tensors, respectively. The tensors  and
and  are used to define general bi-anisotropic, chiral materials , see bi-permittivity and bi-permeability. [1]
are used to define general bi-anisotropic, chiral materials , see bi-permittivity and bi-permeability. [1]
The material is further characterized by the electric conductivity 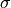 , which relates the electric field intensity to the Ohmic electric current:
, which relates the electric field intensity to the Ohmic electric current:

Transparent boundary conditions
Boundary conditions are an important topic when simulating Maxwell’s equations. In some cases it is justified to prescribe the tangential components of the electric field intensity or of the magnetic field intensity. More generally, an impedance boundary condition relates the tangential components of the electric and magnetic fields, c.f., boundary condition section Electromagnetic.
For high-frequency Maxwell-equations the electromagnetic field radiates over a huge distance of wavelengths into the surrounding of the device without a significant damping. In this case, the computational domain only encloses the device and JCMsolve has to take special care to guarantee field fidelity at the boundaries. In this case, so-called transparent boundaries are to be imposed.
However, within the FEM context of JCMsolve it is more appropriate to think of this transparency not as a boundary condition. Instead, JCMsolve contains numerical methods for solving the problem on the infinite domain. For doing this, a complete description of the physics in the exterior domain has to be passed. This includes the material distribution as well as the incoming electromagnetic field, which illuminates the device. Besides the near field solution, JCMsolve provides post-processes to evaluate the field in the exterior domain and to compute the far field with high precision.
Periodic boundary conditions
Many optical devices such as gratings, photonic crystals or photomasks contain periodic repetitions in one or several directions of a structure filling a unit cell  . To put it in mathematical terms, the material tensors exhibit a translation invariance on a lattice, i.e.:
. To put it in mathematical terms, the material tensors exhibit a translation invariance on a lattice, i.e.:

where  is a lattice vector. Surely, a real world device is not infinitely periodic. However, the periodic arrangement often spreads over a region with a dimension much larger than the wavelength, so that simulating an infinite periodic lattice is a good model.
is a lattice vector. Surely, a real world device is not infinitely periodic. However, the periodic arrangement often spreads over a region with a dimension much larger than the wavelength, so that simulating an infinite periodic lattice is a good model.
To exploit the periodicity in a numerical simulation it is required that the impressed tensor fields exhibit a compatible symmetry condition. Especially, this concerns the source fields 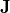 ,
,  and the illuminating electromagnetic field given by the incoming electric and magnetic fields
and the illuminating electromagnetic field given by the incoming electric and magnetic fields  ,
,  :
:

This condition is called Bloch periodicity. The fields are periodic up to a common phase factor  with a common Bloch vector
with a common Bloch vector 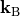 .
.
Lattice vectors  are accompanied by reciprocal lattice vectors
are accompanied by reciprocal lattice vectors  of the same multiplicity, which satisfy
of the same multiplicity, which satisfy

For a one-fold periodicity, i.e., with one single lattice vector  , we demand that
, we demand that  is a multiple of
is a multiple of  . Precisely, we have
. Precisely, we have  . In this case the unit cell may extend infinitely in the directions perpendicular to
. In this case the unit cell may extend infinitely in the directions perpendicular to  or one may impose additional boundary conditions as discussed above.
or one may impose additional boundary conditions as discussed above.
For a two-fold periodicity, one demands that the lattice vectors  ,
, 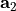 and the reciprocal lattice vectors
and the reciprocal lattice vectors  ,
,  span the same plane with normal
span the same plane with normal 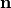 . Again, the unit cell may be infinite in the directions
. Again, the unit cell may be infinite in the directions  or
or  , or it may be bounded by an additional boundary condition.
, or it may be bounded by an additional boundary condition.
Depending quantities
The table below lists field quantities, which are implicitly defined within the solution fieldbag. This way they can be used by subsequent post-processes.
| Quantity | Expression | JCM Tag |
|---|---|---|
| electric flux density |  |
ElectricFluxDensity |
| magnetic flux density |  |
MagneticFluxDensity |
| electric field energy density |  |
ElectricFieldEnergyDensity |
| magnetic field energy density |  |
MagneticFieldEnergyDensity |
| electromagnetic field energy flux (Poynting vector) |  |
ElectromagneticFieldEnergyFluxDensity |
| [1] | We use our own notation  and and  for the bi-anistropic material tensors due to the lack of a standard notation in the literature and a comfortable readability ( for the bi-anistropic material tensors due to the lack of a standard notation in the literature and a comfortable readability ( == “magnetic permittivity”, == “magnetic permittivity”,  == “electric permeability”). == “electric permeability”). |