Function¶
| Type: | string |
|---|---|
| Range: | [] |
| Default: | -/- |
| Appearance: | simple |
| Excludes: | Expression |
Used in combination with Module to specify the python function containing the density field definition.
In the most simple case a Python module is a .py-file which contains one or several python function definition. In this case the name of the module is simply the file name without its .py suffix. The parameter Function is used to pick out the desired function.
The so specified Python function must return a scalar and must accept a single argument which is a dictionary containing the parameters as defined by the Parameter sections.
The syntax is identical to a Python based definition of a source field, see for example the section Function for the definition of an electric field intensity.
As a practical example we want to integrate the electric field energy density  of a time-harmonic electric field intensity
of a time-harmonic electric field intensity 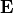 :
:

This density field has two field parameters, namely the electric field intensity 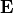 and the complex permittivity tensor
and the complex permittivity tensor  .
.
Tip
It is easier to define this simple example as an inline Python expression as shown in Expression.
Assuming that the respective Python implementation is contained in module PythonTensorFieldLibrary with function name ElectricEnergyDensity, the JCM-syntax looks like this:
DensityIntegration {
FieldBagPath = ...
OutputFileName = ...
Python {
IntegralName = "ElectricEnergy"
Module = "PythonTensorFieldLibrary"
Function = "ElectricEnergyDensity"
Parameter {
Name = "D"
FieldValue {
Quantity = ElectricFluxDensity
}
}
Parameter {
Name = "E"
FieldValue {
Quantity = ElectricFieldStrength
}
}
}
}
In the above, the tag FieldBagPath defines the underlying fieldbag which supplies the meshing for integration. When the underlying fieldbag contains more than one electric field intensities (tagged by ElectricFieldStrength), JCMsolve computes all energies separately.
The used Python function may have the following form:
from numpy import *
def ElectricEnergyDensity(parameters):
D = parameters['D'] # retrieving the D-field vector
E = parameters['E'] # retrieving the E-field vector
return 0.25*dot(D.conj().T, E)
As a second example, we want to compute overlap integrals of the form

This example involves two fieldbags: One fieldbag delivers the 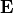 , the other the electric flux density
, the other the electric flux density 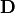 . Surely, the two fieldbags may coincide. The JCM input snippet for this example looks like this:
. Surely, the two fieldbags may coincide. The JCM input snippet for this example looks like this:
DensityIntegration {
FieldBagPath = ... # path to first fieldbag
OutputFileName = ...
Python {
Module = "PythonTensorFieldLibrary"
Function = "ElectricEnergyDensity"
Parameter {
Name = "D"
FieldValue {
Quantity = ElectricFluxDensity
IntegralIndex =1
}
}
Parameter {
Name = "E"
FieldValue {
FieldBagPath = ... # path to second fieldbag
Quantity = ElectricFieldStrength
IntegralIndex =2
}
}
}
}
The Python code is identical to the previous example. However, the field index of the 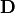 -field parameter runs with the first integral index
-field parameter runs with the first integral index 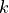 , where as the field index of the VField{E}-fields runs with the second integral index
, where as the field index of the VField{E}-fields runs with the second integral index 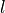 . This way the overlap integrals of all
. This way the overlap integrals of all  -fields in the first fieldbag with all
-fields in the first fieldbag with all 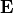 -fields in the second fieldbag are computed.
-fields in the second fieldbag are computed.
As a practical example we want to compute the electromagnetic energy fluxes through domain interfaces of a time-harmonic electromagnetic field. The flux density is the Poynting vector:
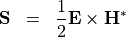
This flux density field has two field parameters, namely the electric field intensity 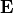 and the magnetic field intensity
and the magnetic field intensity  .
.
Tip
It is easier to define this simple example as an inline Python expression as shown in Expression.
Assuming that the respective Python implementation is contained in module PythonTensorFieldLibrary with function name PoyntingVector, the JCM-syntax looks like this:
The post-process may be defined as follows:
DensityIntegration { FieldBagPath = ... OutputFileName = ... InterfaceType = ... Module = "PythonTensorFieldLibrary" Function = "PoyntingVector" Python { IntegralName = "ElectromagneticEnergyFlux" Parameter { Name = "E" FieldValue { Quantity = ElectricFieldStrength } } Parameter { Name = "H" FieldValue { Quantity = MagneticFieldStrength } } } }In the above, the tag
FieldBagPathdefines the underlying fieldbag which supplies the meshing for integration. When the underlying fieldbag contains more than one electromagnetic fields,JCMsolvecomputes all fluxes separately. When choosingInterfaceType=ExteriorDomainthe scattered fieldsand
are passed on the interior-exterior domain interfaces.
The used Python function may have the following form:
from numpy import * def ElectricEnergyDensity(parameter): E = parameter['E'] # retrieving the E-field vector H = parameter['E'] # retrieving the H-field vector return 0.5*cross(E, H)As a second example, we want to compute overlap integrals of the form
on the cross-section domains of a two-dimensional problem with an infinite
-direction. This requires to set
InterfaceType=CrossSection.This example involves two fieldbags: One fieldbag delivers the electric field
, the other the magnetic field
. The two fieldbags may coincide. The JCM input snippet for this example looks like this:
DensityIntegration { FieldBagPath = ... # path to first fieldbag OutputFileName = ... InterfaceType = CrossSection Python { IntegralName = "OverlapCrossSectionEnergyFlux" Module = "PythonTensorFieldLibrary" Function = "PoyntingVector" Parameter { Name = "E" FieldValue { Quantity = ElectricFieldStrength } } Parameter { Name = "H" FieldValue { FieldBagPath = ... # path to second fieldbag Quantity = MagneticFieldStrength } } } }The Python code is identical to the previous example. However, the field index of the
-field parameter runs with the first integral index
, where as the field index of the
-fields runs with the second integral index
. This way the overlap flux integrals of all
-fields in the first fieldbag with all
-fields in the second fieldbag are computed.