RelPermittivity¶
| Type: | 2-Tensor, or section |
|---|---|
| Range: | [v_1, …, v_9] |
| Default: | [1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0] |
| Appearance: | simple |
Specifies the relative permittivity 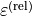 . The relative permittivity is dimensionless. It defines the permittivity as
. The relative permittivity is dimensionless. It defines the permittivity as 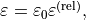 where
where  is the vacuum permittivity in units farads per meter,
is the vacuum permittivity in units farads per meter, 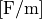 (which equals to units coulomb per volt per meter,
(which equals to units coulomb per volt per meter, 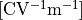 ).
The permittivity
).
The permittivity  relates the electric displacement
relates the electric displacement  to the electric field strength
to the electric field strength  ,
,
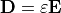
For the extension to bi-anistropic materials see RelBiPermittivity.
A constant relative permittivity can be defined by assigning a rank-2 tensor:
Material {
# defines a constant relative permittivity
RelPermittivity =
[..., ..., ...
..., ..., ...
..., ..., ...]
}
Assign a scalar for an isotropic relative permittivity:
Material {
...
RelPermittivity = 2.25
}
For more general cases, the relative permittivity may be given as a section in order to deal with space, time, frequency and parameter dependent definitions:
# define the relative permittivity as a section
RelPermittivity {
Python {...}
PhotoElasticCorrection { ... }
ThermoOpticalCorrection { ... }
...
}
Field definitions within the section RelPermittivity are summed up. Consult the subsequent sections to see which types of field definitions are allowed.
Note
The refractive index (index of refraction, 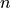 ) of an
optical medium relates to the relative permittivity
) of an
optical medium relates to the relative permittivity
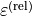 and relative
permeability
and relative
permeability  as
as
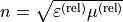 .
In most cases,
.
In most cases,  .
Therefore, e.g., for an isotropic material with refractive index
.
Therefore, e.g., for an isotropic material with refractive index  ,
the relative permittivity is specified as
,
the relative permittivity is specified as RelPermittivity = 2.25.
Lossy materials can be modeled using a complex refractive index, 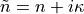 ,
with
,
with  , e.g.,
, e.g., 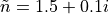 . In this example, a complex relative permittivity is specified:
. In this example, a complex relative permittivity is specified: RelPermittivity = 2.24+0.3i.
(Please note the sign convention, where a positive  relates to absorption, c.f.,
TimeHarmonic.)
relates to absorption, c.f.,
TimeHarmonic.)