PhotoElasticCorrection¶
| Type: | section |
|---|---|
| Appearance: | multiple |
The photo-elastic correction relates the stresses within a body to a change of the relative permittivity. To formulate this correction term it is necessary to bring the stress tensor 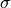 , given by a symmetric
, given by a symmetric 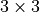 - matrix, into diagonal form using a coordinate rotation
- matrix, into diagonal form using a coordinate rotation  :
:
![\begin{eqnarray*}
\TField{\sigma} & = & \TField{R} \cdot \left [ \begin{array}{ccc}
\sigma_{x'x'} & 0 & 0 \\
0 & \sigma_{y'y'} & 0 \\
0 & 0 & \sigma_{z'z'}
\end{array} \right] \cdot \TField{R}^{\mathrm{T}}
\end{eqnarray*}](_images/math/b604d826fea0c668cb455c0c84ff0f0ad9ca277c.png)
The columns of the rotation matrix 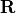 are the three principle axes of the stress tensor and
are the three principle axes of the stress tensor and  ,
,  and
and  are the stresses into the directions of the principle axes.
are the stresses into the directions of the principle axes.
Within the  - coordinate system the photo-elastic correction is in diagonal form and is given as follows:
- coordinate system the photo-elastic correction is in diagonal form and is given as follows:

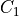 and
and 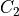 are called photo-elastic constants. The first coefficient
are called photo-elastic constants. The first coefficient 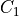 relates the stress in the direction of a principle axis to a permittivity change in this direction, whereas
relates the stress in the direction of a principle axis to a permittivity change in this direction, whereas 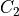 gives rise to a permittivity correction perpendicular to the considered principle axis.
gives rise to a permittivity correction perpendicular to the considered principle axis.
Transforming to the original  - coordinate system we get that
- coordinate system we get that
![\begin{eqnarray*}
\Delta \TField{\varepsilon}^{(\mathrm{rel})} & = & \TField{R} \cdot \left [ \begin{array}{ccc}
\Delta \TField{\varepsilon}^{(\mathrm{rel})}_{x'x'} & 0 & 0 \\
0 & \Delta \TField{\varepsilon}^{(\mathrm{rel})}_{y'y'} & 0 \\
0 & 0 & \Delta \TField{\varepsilon}^{(\mathrm{rel})}_{z'z'}
\end{array} \right] \cdot \TField{R}^{\mathrm{T}}.
\end{eqnarray*}](_images/math/3350e0fa274eb4caf81a29b2ee84cec5ca12dfae.png)
The full relative permittivity is then given by

where  is the relative permittivity of the stress free body.
is the relative permittivity of the stress free body.
For too large stresses the linear correction term may loose its validity. Especially, extremely large stresses occurs near corners of the geometry, where the stress may exhibit field singularities. To prevent obscure relative permittivity definitions one may restrict the absolute value of the correction term by a threshold value  ,
,

The JCM - syntax looks like this:
# define the relative permittivity with photo-elastic correction
RelPermittivity {
# define relative permittivity of stress free body
Constant = ...
...
PhotoElasticCorrection {
C1 = ... # set first photo-elastic coefficient
C2 = ... # set second photo-elastic coefficient
CutOff .. # set threshold here
}
}
Warning
Often, the photo-elastic coefficient is defined as a refractive index - stress relation.
In a linear sense the refractive index based definition is equivalent to the definition in JCMsuite: In the  - coordinate system the refractive index change be given by
- coordinate system the refractive index change be given by

and corresponding expression for  and
and 
With the refractive index  of the stress-free body this results in the following definition of the relative permittivity:
of the stress-free body this results in the following definition of the relative permittivity:

The approximation in the last line is due to linearization. The last line is precisely the definition of the photo-elastic relation in JCMsuite when setting  and
and 