FieldComponents¶
| Type: | enum |
|---|---|
| Range: | Electric, ElectricXYZ, ElectricXZ, ElectricY, Magnetic, MagneticXYZ, MagneticXZ, MagneticY, Scalar-MagneticX, Scalar-MagneticY |
| Default: | Electric |
| Appearance: | simple |
Specifies which field components should be computed. The allowed choices have the following meanings:
ElectricXYZ and MagneticXYZ
Use this for rigorous Maxwell solutions with a two-dimensional cross-section.
In the first case, the full second order equations for the electric field are solved, yielding a hybrid electric mode where all components are non-zero, see here. In the second case the analogue magnetic field equations are used. Since both settings are derived directly from Maxwell’s equations they yield identical propagation constants  . The electric and magnetic fields can be computed from each other by applying Maxwell’s equations.
. The electric and magnetic fields can be computed from each other by applying Maxwell’s equations.
Scalar-MagneticX and Scalar-MagneticY
Use this for a scalar approximation of Maxwell’s equations (weak guidance approximation, c.f., [1]). The approximation is only valid for low-contrast refractive index profiles. When using Scalar-MagneticX the  and
and  components of the magnetic field are neglected. This allows to simplify Maxwell’s equations to derive a scalar equation for
components of the magnetic field are neglected. This allows to simplify Maxwell’s equations to derive a scalar equation for  . The choice
. The choice Scalar-MagneticY is treated in an analogue way, but now only the  components is non-zero.
components is non-zero.
ElectricY, MagneticXZ and MagneticY, ElectricXZ
Use these for slab problems with a one-dimensional grid field grid.jcm. For all choices rigorous Maxwell’s equations are solved.
When setting ElectricY, modes with vanishing electric 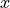 and
and  -components are computed. In this case Maxwell’s equations simplifies to a scalar equation for
-components are computed. In this case Maxwell’s equations simplifies to a scalar equation for 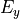 in a rigorous manner. The corresponding magnetic field has a vanishing
in a rigorous manner. The corresponding magnetic field has a vanishing  -component and can be computed directly when setting
-component and can be computed directly when setting MagneticXZ. Hence, setting ElectricY and MagncticXZ yield identical propagation constants  .
.
The considerations for MagneticY and ElectricXZ are similar.
Bibliography
| [1] | N.J. Cronin, Microwave and optical waveguides, Institute of Physics Publishing, 1995. |