RelBiPermittivity¶

Type:	2-Tensor, or section
Range:	[v_1, …, v_9]
Default:	-/-
Appearance:	optional

This parameter specifies the relative magnetic permittivity (the coupling between the electric displacement 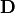$\VField{D}$ field and the magnetic field 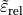$\VField{H}$ ) $\tilde{\TField{\varepsilon}}_{\mathrm{rel}}$ as follows:

$\begin{alignat*}{1} \tilde{\TField{\varepsilon}} &= \tilde{\TField{\varepsilon}}_{\mathrm{rel}} \sqrt{\varepsilon_0\mu_0} \end{alignat*}$

Warning

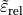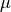Usually the relative magnetic permittivity $\tilde{\TField{\varepsilon}}_{\mathrm{rel}}$ is defined relative to the background permittivity and permeability. We do not follow this convention as it is not clear how this convention is applied for general an-isotropic tensors $\TField{\varepsilon}$ and $\TField{\mu}$ .

For general bi-anisotropic materials the material constitutive relations read as

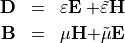
$\begin{alignat*}{2} \VField{D} \phantom{x} &= \phantom{x} \TField{\varepsilon} \VField{E} & + \tilde{\TField{\varepsilon}} \VField{H} \\ \VField{B} \phantom{x} &= \phantom{x} \TField{\mu} \VField{H} & + \tilde{\TField{\mu}} \VField{E} \end{alignat*}$

Typically the tensors $\tilde{\TField{\varepsilon}}$ and $\tilde{\TField{\mu}}$ are not independent from each other. To preserve reciprocity of Maxwell’s equation it is required that

$\begin{alignat*}{1} \tilde{\TField{\varepsilon}} & = -\tilde{\TField{\mu}}^{\mathrm{T}} \end{alignat*}$

For a bi-anisotropic material without damping additional to the Ohmic losses we have

$\begin{alignat*}{1} \tilde{\TField{\varepsilon}} & = \tilde{\TField{\mu}}^{\mathrm{H}}. \end{alignat*}$

Isotropic materials are typically classified by the reciprocity parameter 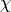$\chi$ and the chirality parameter $\kappa$ ,

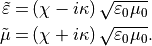
$\begin{alignat*}{1} \tilde{\TField{\varepsilon}} = & \left(\chi-i\kappa\right)\sqrt{\varepsilon_0 \mu_0} \\ \tilde{\TField{\mu}} = & \left(\chi+i\kappa\right)\sqrt{\varepsilon_0 \mu_0}. \end{alignat*}$

This material definition introduces no additional losses and is reciprocal for 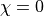$\chi = 0$ .