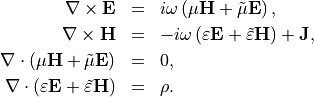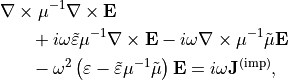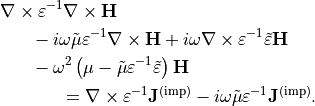TimeHarmonic¶
| Type: | section |
|---|---|
| Appearance: | simple |
This section is used to describe an electromagnetic field problem in the frequency domain. This means that the electromagnetic field depends harmonically on time with an angular frequency 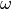 . The relevant fields are replaced by complex phasors
. The relevant fields are replaced by complex phasors 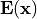 ,
, 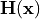 , etc., related to the actual fields by
, etc., related to the actual fields by

This allows to write Maxwell’s equations as
When splitting the electric current into the ohmic current 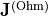 and the impressed current
and the impressed current 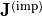 , that is
, that is
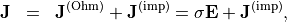
the second equation reads as
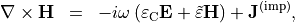
with the complex permittivity tensor
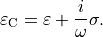
In the context of time-harmonic problems the index ‘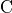 ’ will be dropped and it should be kept in mind that the permittivity tensor is allowed to have complex-valued entries.
’ will be dropped and it should be kept in mind that the permittivity tensor is allowed to have complex-valued entries.
From this one obtains independent equations of second order for the electric and magnetic fields:
and