MultipoleExpansion¶
Use this post-process to obtain the multipole expansion of a time-harmonic electromagnetic field in a lossless homogeneous isotropic exterior.
In a nutshell, the outgoing electromagnetic field is determined and decomposed into contributions from various spherical vector waves or multipoles. These radiate radially outwards, thus fulfilling the Sommerfeld radiation conditions, and travel towards infinity.
Example: A multipole expansion post-process may be specified as follows:
PostProcess {
MultipoleExpansion {
FieldBagPath = "./project_results/fieldbag.jcm"
OutputFileName = "./project_results/expansion_coefficients.jcm"
Format = JCM-ASCII
MultipoleDegree = 2
}
}
Theoretical background
It is required that the scatterer is surrounded by a lossless, homogeneous and isotropic material distribution enclosing the origin. Let 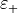 and
and 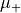 denote the corresponding scalar permittivity and permeability, respectively. The angular wave number is given by
denote the corresponding scalar permittivity and permeability, respectively. The angular wave number is given by 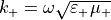 . In this setting, the scattered electromagnetic field at a point
. In this setting, the scattered electromagnetic field at a point  can be expanded into a basis of vector spherical wave functions which are orthonormal on the unit sphere
can be expanded into a basis of vector spherical wave functions which are orthonormal on the unit sphere 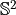 .
.
![\begin{eqnarray*}
\VField{E}_{sc}(\pvec{r},k_+) = \sum_{n=1}^{\infty} \sum_{m=-n}^n \left[ a_{nm}\pvec{N}_{nm}(\pvec{r},k_+) + b_{nm}\pvec{M}_{nm}(\pvec{r},k_+ )\right].
\end{eqnarray*}](_images/math/220d4aeb4fe16dbc74b037f119c90ac2a5116c1b.png)
The coefficients 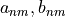 are determined by the following integrals
are determined by the following integrals
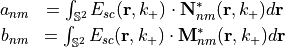
The vector spherical wave functions 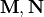 for the outgoing fields have the following definition in terms of spherical coordinates
for the outgoing fields have the following definition in terms of spherical coordinates 
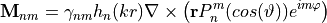
![\begin{eqnarray*}
\pvec{N}_{nm} = \frac{1}{k} \nabla \times \pvec{M}_{nm} = \gamma_{nm} \left[ \frac{n(n+1)}{kr}h_{n}(kr) \frac{\pvec{r}}{r} P_{n}^m(cos(\vartheta))e^{im\varphi} + \frac{r}{kr} \frac{d}{d(kr)}\left(kr h_n(kr)\right) \nabla \left( P_{n}^m(cos(\vartheta))e^{im\varphi} \right) \right]
\end{eqnarray*}
with the common normalization factor](_images/math/456c9d0fd62628098eacc60f0b8024ebe83c8ef8.png)
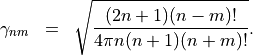
The definition makes use of the spherical Hankel functions of the first kind 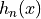 and the associated Legendre polynomials
and the associated Legendre polynomials 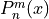 of degree
of degree 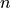 and order
and order 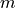 .
.
Storage format
The computed multipole expansion is stored in a JCM table. Each row in the table corresponds to a vector spherical wave function. Summing up (superimposing) these spherical waves gives an approximation of the scattered field:
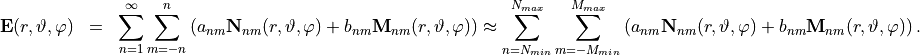
The type (electric or magnetic multipole moments) is stored on the first columns as a binary variable. The output JCM table file has the following columns:
Columns 1: Type
This is type of the vector spherical wave function
 or
or 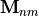 (as explained above) encoded in a binary variable: 1 indicates
(as explained above) encoded in a binary variable: 1 indicates  type and a 0
type and a 0 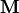 type.
type.Columns 2-3: n, m
The second and third columns contain the integer multipole degree
nand ordermof the vector spherical wave function .
.Columns …: ExpansionCoefficient_<iF>, …
The subsequent columns contain the expansion coefficients
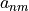 or
or  of the respective vector spherical wave function. The index
of the respective vector spherical wave function. The index <iF>stands for the field index.