Zernike Polynomials¶
The Zernike polynomials  are a complete sequence of polynomials that are orthogonal on the unit disk. Using polar coordinates
are a complete sequence of polynomials that are orthogonal on the unit disk. Using polar coordinates 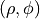 , so that
, so that  , the Zernike polynomials are defined as
, the Zernike polynomials are defined as
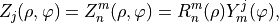
with
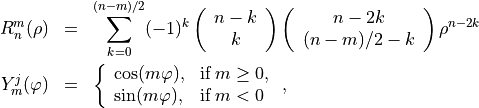
and where the integer index pair  is given by
is given by
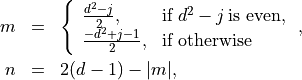
where 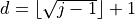 , and
, and  represents the largest integer that is less or equal to the delimited integer.
represents the largest integer that is less or equal to the delimited integer.
Warning
Different orderings  of the Zernike polynomials are in use. Here, we followed
[1] (page 213). Besides this, different scalings of the Zernike polynomials are used.
of the Zernike polynomials are in use. Here, we followed
[1] (page 213). Besides this, different scalings of the Zernike polynomials are used.
In the above, the Fringe convention as been used for scaling (c.f. http://en.wikipedia.org/wiki/Zernike_polynomials or http://mathworld.wolfram.com/ZernikePolynomial.html). For the sake of clarity, the following table lists the leading 36 (Fringe)-Zernike polynomials:
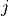 |
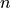 |
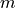 |
 |
description |
|---|---|---|---|---|
| 1 | 0 | 0 | 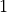 |
piston |
| 2 | 1 | 1 | 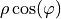 |
x-tilt |
| 3 | 1 | -1 |  |
y-tilt |
| 4 | 2 | 0 | 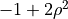 |
defocus |
| 5 | 2 | 2 | 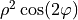 |
astigmatism |
| 6 | 2 | -2 | 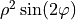 |
astigmatism |
| 7 | 3 | 1 | 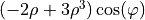 |
coma |
| 8 | 3 | -1 | 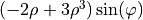 |
coma |
| 9 | 4 | 0 | 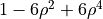 |
spherical aberration |
| 10 | 3 | 3 | 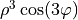 |
trifoil |
| 11 | 3 | -3 | 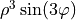 |
trifoil |
| 12 | 4 | 2 | 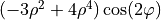 |
astigmatism |
| 13 | 4 | -2 | 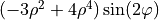 |
astigmatism |
| 14 | 5 | 1 | 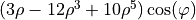 |
coma |
| 15 | 5 | -1 | 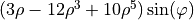 |
coma |
| 16 | 6 | 0 |  |
spherical aberration |
| 17 | 4 | 4 | 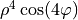 |
four wave |
| 18 | 4 | -4 |  |
four wave |
| 19 | 5 | 3 |  |
trifoil |
| 20 | 5 | -3 | 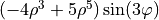 |
trifoil |
| 21 | 6 | 2 | 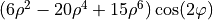 |
astigmatism |
| 22 | 6 | -2 | 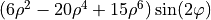 |
astigmatism |
| 23 | 7 | 1 | 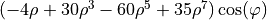 |
coma |
| 24 | 7 | -1 | 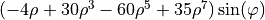 |
coma |
| 25 | 8 | 0 | 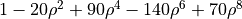 |
spherical aberration |
| 26 | 5 | 5 |  |
five wave |
| 27 | 5 | -5 | 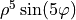 |
five wave |
| 28 | 6 | 4 | 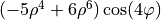 |
four wave |
| 29 | 6 | -4 | 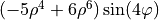 |
four wave |
| 30 | 7 | 3 | 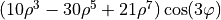 |
trifoil |
| 31 | 7 | -3 |  |
trifoil |
| 32 | 8 | 2 | 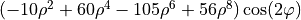 |
astigmatism |
| 33 | 8 | -2 | 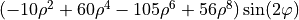 |
astigmatism |
| 34 | 9 | 1 | 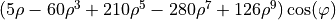 |
coma |
| 35 | 9 | -1 | 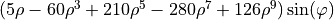 |
coma |
| 36 | 10 | 0 | 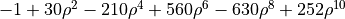 |
spherical aberration |
Bibliography
| [1] | Gross H. (editor), Handbook of Optical Systems, Volume III, Wiley-VCH 2005 |