Superellipse¶
| Type: | section |
|---|---|
| Appearance: | multiple |
A superellipse is a planar, closed curve in the rectangle ![x \in [-R_x,R_x] , y \in [-R_y,R_y]](_images/math/4218c056859da5ba8511a85efcb332cd708300e5.png) . It can be viewed as a generalization of the ellipse as it retains the symmetry properties about the semi-major and semi-minor axes. All points on the curve satisfy the following equation
. It can be viewed as a generalization of the ellipse as it retains the symmetry properties about the semi-major and semi-minor axes. All points on the curve satisfy the following equation
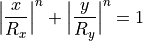
The ellipse is a special case of this equation with 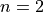 . For
. For 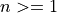 convex curves are obtained. Examples are the rhombus (
convex curves are obtained. Examples are the rhombus (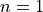 ) or a curve resembling a rounded rectangle (
) or a curve resembling a rounded rectangle (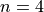 ) shown below. Concave curves, like the four armed star shown below, are a result of exponents
) shown below. Concave curves, like the four armed star shown below, are a result of exponents  .
.
