RoughSurface¶
| Type: | section |
|---|---|
| Appearance: | optional |
| Excludes: | Python, Triangulation |
Here, it is possible to define a texture as a synthetic randomized rough surface. This rough surface height profile 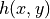 creation is based on a centralized Gaussian distribution in space,
creation is based on a centralized Gaussian distribution in space,
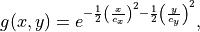
which is randomly displaced while summed up and normalized. This process can be written in terms of the forward and backward Fourier transform (denoted by 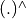 and
and 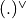 ) as follows:
) as follows:

The phase function 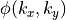 is randomly chosen, or by an deterministic pseudo random number generator when setting the seed for the random number generator (see RandomSeed).
is randomly chosen, or by an deterministic pseudo random number generator when setting the seed for the random number generator (see RandomSeed).
The scaling factor 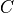 is determined, so that the root mean square of the height profile function,
is determined, so that the root mean square of the height profile function,
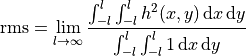
equals the value passed in RMSHeight.
Note
In case of a periodic computational domain the rough surface is constructed in a periodified manner.