NumericalAperture¶

Type:	float
Range:	[0, inf]
Default:	-/-
Appearance:	optional

The numerical aperture 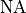$\mathrm{NA}$ restricts the Fourier spectrum which is allowed to pass. With the notation of the parent section OpticalSystem, a ray passing the optical system must satisfies

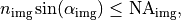
$\begin{eqnarray*} n_\mathrm{img} \sin(\alpha_\mathrm{img}) \leq \mathrm{NA}_\mathrm{img}, \end{eqnarray*}$

or, equivalently

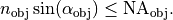
$\begin{eqnarray*} n_\mathrm{obj} \sin(\alpha_\mathrm{obj}) \leq \mathrm{NA}_\mathrm{obj}. \end{eqnarray*}$

The discussed parameter 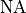$\mathrm{NA}$ refers to the image side numerical aperture 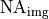$\mathrm{NA}_\mathrm{img}$ for diminishing systems with magnification 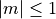$|m|\leq 1$ , and to the object side numerical aperture 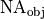$\mathrm{NA}_\mathrm{obj}$ for magnifying systems, in order to match the standard conventions used in photolithography and microscopy respectively.

In terms of the pupil function 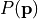$P(\pvec{p})$ with normalized coordinates 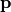$\pvec{p}$ this means that

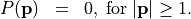
$\begin{eqnarray*} P(\pvec{p}) & = & 0,\; \mbox{for}\; |\pvec{p}|\geq 1. \end{eqnarray*}$

From the discussion in the previous section it follows that the maximum numerical aperture is 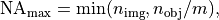$\mathrm{NA}_{\mathrm{max}}=\min(n_{\mathrm{img}}, n_{\mathrm{obj}}/m),$ since evanescent waves cannot pass. In practice, the numerical aperture is further restricted by the openings of the optical system.

Compare also the parameter InnerNumericalAperture which blocks all Fourier modes with smaller NA than the specified value.