Parameter Reconstruction¶
In this tutorial we briefly discuss how we can perform a parameter reconstruction using a Mueller matrix ellipsometry dataset. We use the same project files that were also used in the discussion on Mueller matrix ellipsometry in the EM tutorial example.
We assume that we have acquired a set of measurements from a Mueller matrix ellipsometry
experiment on a grating, that was performed for a series of different incident light
wavelengths 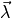 . These measurements are arranged in a target vector
. These measurements are arranged in a target vector
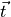 , for which we know which Mueller matrix element for which wavelength is
found where in this vector. We further assume that we can assign a measurement uncertainty
to each of the components in
, for which we know which Mueller matrix element for which wavelength is
found where in this vector. We further assume that we can assign a measurement uncertainty
to each of the components in 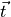 , we denote the measurement uncertainty vector
as
, we denote the measurement uncertainty vector
as 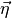 . Please note that the actual ordering of the components within the
vector is of no importance for the reconstruction.
. Please note that the actual ordering of the components within the
vector is of no importance for the reconstruction.
The information contained in the target vector 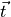 can be used to infer the
geometrical parameters of the investigated grating. This can be done by solving an inverse
problem. The approach for this is as follows. A parameterized model of the measurement
process is created. The model parameters are then varied in a systematic fashion, until a
set of model parameters is determined for which the calculated output of the model is
similar to the set of experimental measurements of the grating.
can be used to infer the
geometrical parameters of the investigated grating. This can be done by solving an inverse
problem. The approach for this is as follows. A parameterized model of the measurement
process is created. The model parameters are then varied in a systematic fashion, until a
set of model parameters is determined for which the calculated output of the model is
similar to the set of experimental measurements of the grating.
The parameterized model for the Mueller matrix ellipsometry experiment is created using
JCMsuite. A function is created which computes the Mueller matrix entries 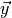 using the FEM model for the same set of incident wavelengths
using the FEM model for the same set of incident wavelengths 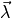 that
were used during the actual experiment. This involves the Fourier transformation and the
scattering matrix postprocesses discussed in the EM tutorial. The various matrix entries
are assembled in a vector
that
were used during the actual experiment. This involves the Fourier transformation and the
scattering matrix postprocesses discussed in the EM tutorial. The various matrix entries
are assembled in a vector 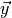 with the same ordering as the target vector
with the same ordering as the target vector
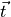 , and then returned.
, and then returned.
The actual parameter reconstruction, that is the fit of the model output to the target
vector, can efficiently be performed using the BayesLeastSquare driver of the analysis and
optimization toolbox within the Driver Reference. The approach is closely related to Bayesian
optimization and similarly employs Gaussian processes (a machine learning surrogate
model), and allows to perform a global black box optimization of the least-squares
problems. By using Gaussian processes the method is very well suited for expensive model
functions, such as a wavelength dependent Mueller matrix calculation and is capable of
finding a set of model parameters that explain the experiment in fewer iterations than
conventional methods. An in-depth discussion and explanation of the approach is presented
in an article on
our Blog.
The optimization script is set up in a very similar fashion as the one in the Optimization tutorial. The complete script looks as follows.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 | % Add JCMsuite to MATLAB path
jcm_root = getenv('JCMROOT'); % Linux: use: jcm_root = <JCMROOT> -> set your JCMROOT installation directory
addpath(fullfile(jcm_root, 'ThirdPartySupport', 'Matlab'));
%% Shutdown a possibly running daemon
jcmwave_daemon_shutdown();
% Parameters to play with
NUM_ITERATIONS = 20;
DERIVATIVE_ORDER = 1;
FEM_DEGREE = 3;
MULTIPLICITY = 1; % max of 1 for demo version
%% Register a new computer resource
jcmwave_daemon_add_workstation('Hostname', 'localhost', ...
'Multiplicity', MULTIPLICITY, ...
'NThreads', 2);
% Main script
% Define the paths
root_dir = fileparts(mfilename('fullpath'));
data_dir = fullfile(root_dir, 'data');
project_file = fullfile(root_dir, 'jcm', 'project.jcmp');
% Model parameters
model_param_keys = struct('h', 55, 'width', 31, 'swa', 88, 'radius', 8);
% Rest of the parameters for the JCMsuite project
keys = struct('derivative_order', DERIVATIVE_ORDER, 'fem_degree', FEM_DEGREE, 'precision', 1e-3, ...
'n1', 1, 'n2', 1.4, 'n3', 1.967 + 4.443 * 1i, ...
'theta', 65, 'phi', 45, 'vacuum_wavelength', 365e-9);
% Merge the two
keys = mergeStructs(keys, model_param_keys);
% Load the material data
material = loadSiMaterial(data_dir);
% Define wavelengths
wl_count = 11;
wavelengths = linspace(266, 800, wl_count);
% Define the optimization domain
optimization_domain = struct('name', {'h', 'width', 'swa', 'radius'}, ...
'type', {'continuous', 'continuous', 'continuous', 'continuous'}, ...
'domain', {[50, 60], [25, 35], [84, 90], [6, 8]});
% Load target parameters and values
[target_keys, target_vector, uncertainty_vector] = loadTargetData(data_dir);
% Set up the study
study_id = 'Ellipsometry_reconstruction_example';
optimization_dir = fileparts(mfilename('fullpath'));
study = setupStudy(optimization_domain, study_id, optimization_dir);
% Define the objective function
objective = @(params) objectiveFunction(params, keys, optimization_domain, project_file, wavelengths, material, study);
% Set study parameters
study.set_parameters('target_vector', target_vector', ...
'uncertainty_vector', uncertainty_vector', ...
'max_iter', NUM_ITERATIONS);
fprintf('\n\n');
fprintf('The target parameter to be reconstructed is\n');
for i = 1:length(optimization_domain)
parameter_name = optimization_domain(i).name;
fprintf('\t%s: %g\n', parameter_name, target_keys.Value(i));
end
fprintf('\n');
if keys.derivative_order > 0
fprintf('Derivative information of the FEM solver is being used\n');
else
fprintf('Derivative information of the FEM solver is not being used\n');
end
fprintf('\n');
% Run the minimization
while(not(study.is_done))
sug = study.get_suggestion();
obs = objective(sug.sample);
study.add_observation(obs, sug.id);
end
% Plot the reconstruction results and compare to target
plotReconstructionResults(study, target_vector, uncertainty_vector, wavelengths, optimization_dir, project_file, keys, material);
% Helper functions
function result = mergeStructs(struct1, struct2)
% Merge two structures into one
result = struct1;
fields = fieldnames(struct2);
for i = 1:numel(fields)
result.(fields{i}) = struct2.(fields{i});
end
end
function material = loadSiMaterial(data_dir)
material_file = fullfile(data_dir, 'Aspnes.csv');
% Read the material file
n_data = readtable(material_file, 'Range', 'A2:B47');
k_data = readtable(material_file, 'Range', 'A49:B94');
% Create interpolators for material data
material.n_interpolator = griddedInterpolant(n_data{:, 1} * 1e3, n_data{:, 2}, 'linear');
material.k_interpolator = griddedInterpolant(k_data{:, 1} * 1e3, k_data{:, 2}, 'linear');
end
function nk = get_nk(material, wavelength)
nk = material.n_interpolator(wavelength) + 1i * material.k_interpolator(wavelength);
end
function [mueller_matrices, mueller_matrices_derivatives] = solve_forward_problem(project_file, wavelengths, material, keys)
job_ids = [];
for wavelength = wavelengths
% Get a local copy of the keys for modifying and dispatching
inner_keys = keys;
inner_keys.vacuum_wavelength = wavelength * 1e-9;
inner_keys.n3 = get_nk(material, wavelength);
job_id = jcmwave_solve(project_file, inner_keys, 'temporary', 'yes');
job_ids = [job_ids, job_id];
end
% Here we wait until all jobs are finished
[results, logs] = jcmwave_daemon_wait(job_ids); % Assuming a similar function exists
% Initialize mueller_matrices
mueller_matrices = zeros(length(wavelengths), 4, 4);
% Iterate over all results
for idx = 1:length(results)
result = results{idx};
% First get the Mueller matrix
M = result{3}.Mueller_ps; % Corrected indexing
% Extract the 4x4 matrix from the cell array
M_matrix = M{1};
mueller_matrices(idx, :, :) = M_matrix;
end
% Initialize derivatives
mueller_matrices_derivatives = struct();
param_names = {'h', 'width', 'swa', 'radius'};
for p = 1:length(param_names)
param = param_names{p};
derivative_key = ['d_', param];
param_derivative = zeros(length(wavelengths), 4, 4);
for idx = 1:length(results)
result = results{idx};
if isfield(result{3}, derivative_key)
dM = result{3}.(derivative_key).Mueller_ps{1};
param_derivative(idx, :, :) = dM;
end
end
mueller_matrices_derivatives.(param) = param_derivative;
end
end
function [target_keys, target_vector, uncertainty_vector] = loadTargetData(data_dir)
% Load target parameters
target_keys_table = readtable(fullfile(data_dir, 'target_parameters.csv'));
target_keys = table2struct(target_keys_table, 'ToScalar', true);
% Load target values
target_values = readtable(fullfile(data_dir, 'target_values.csv'));
target_vector = target_values.target_vector;
uncertainty_vector = target_values.uncertainty_vector;
end
function study = setupStudy(optimization_domain, study_id, optimization_dir)
client = jcmwave_optimizer_client();
study = client.create_study('domain', optimization_domain, ...
'driver', 'BayesLeastSquare', ...
'name', 'Ellipsometry reconstruction example', ...
'study_id', study_id, ...
'save_dir', optimization_dir, ...
'open_browser', true);
end
function observation = objectiveFunction(params, keys, optimization_domain, project_file, wavelengths, material, study)
% Merge the new parameters with the existing ones
objective_keys = mergeStructs(keys, params);
% Solve the forward problem
[mueller_matrix, mueller_matrix_derivatives] = solve_forward_problem(project_file, wavelengths, material, objective_keys);
% Create a new observation
observation = study.new_observation();
% Add the Mueller matrix
flat_mueller_matrix = flatten_C_style(mueller_matrix);
observation.add(flat_mueller_matrix');
% Add derivatives if available
if objective_keys.derivative_order > 0
for p = 1:length(optimization_domain)
parameter = optimization_domain(p);
if strcmp(parameter.type, 'continuous')
derivative_value = flatten_C_style(mueller_matrix_derivatives.(parameter.name));
observation.add(derivative_value', parameter.name);
end
end
end
end
function plotReconstructionResults(study, target_vector, uncertainty_vector, wavelengths, optimization_dir, project_file, keys, material)
% Reshape target and uncertainty vectors
target_matrix = reshape(target_vector, 4, 4, length(wavelengths));
% Get the minimum parameters
study_info = study.info();
min_params = study_info.min_params;
keys = mergeStructs(keys, min_params);
% Generate reconstruction data for comparison
[reconstructed_mueller_matrix, ~] = solve_forward_problem(project_file, wavelengths, material, keys);
flat_reconstructed_mueller_matrix = flatten_C_style(reconstructed_mueller_matrix)';
reconstructed_mueller_matrix = reshape(flat_reconstructed_mueller_matrix, 4, 4, length(wavelengths));
% Plot the results
fig = figure;
tiledlayout(4, 4, 'TileSpacing', 'Compact');
sgtitle('Mueller matrix entries');
for i = 1:4
for j = 1:4
nexttile;
plot(wavelengths, squeeze(target_matrix(j, i, :)), 'DisplayName', 'Target');
hold on;
plot(wavelengths, squeeze(reconstructed_mueller_matrix(j, i, :)), 'DisplayName', 'Reconstructed');
hold off;
title(['M' num2str(i) num2str(j)]);
if i == 4
xlabel('Wavelength (nm)');
end
end
end
legend('show');
saveas(fig, fullfile(optimization_dir, 'reconstruction.png'));
end
% The target dataset was created using numpy, which uses a different array flattening
% scheme. Hence, we have to account for this and flatten arrays in matlab in C style as
% opposed to F style.
function flattened_C_style_list = flatten_C_style(matrices)
% Initialize an empty array to store the flattened results
flattened_C_style_list = [];
% Get the size of the first dimension
num_matrices = size(matrices, 1);
% Iterate over each slice of the 3D array
for k = 1:num_matrices
matrix = squeeze(matrices(k, :, :));
% Transpose the matrix to switch row-major to column-major
matrix_T = matrix';
% Flatten the transposed matrix and concatenate
flattened_C_style_list = [flattened_C_style_list; matrix_T(:)];
end
end
|
To perform the fit we provide to the optimizer a target vector to which we want to fit the model, and optionally an uncertainty vector which contains the measurement uncertainties associated with each component of the target vector.
63 64 65 66 | % Set study parameters
study.set_parameters('target_vector', target_vector', ...
'uncertainty_vector', uncertainty_vector', ...
'max_iter', NUM_ITERATIONS);
|
The optimized objective function computes not a single scalar value but a list of values
that are added to an observation. At each iteration, this vector valued observation is
evaluated. Derivatives can be used to speed up the reconstruction process. As such, the
JCMsuite project is set up to also return parameter derivatives. These are added to the
observation at each iteration.
60 61 | % Define the objective function
objective = @(params) objectiveFunction(params, keys, optimization_domain, project_file, wavelengths, material, study);
|
193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 | function observation = objectiveFunction(params, keys, optimization_domain, project_file, wavelengths, material, study)
% Merge the new parameters with the existing ones
objective_keys = mergeStructs(keys, params);
% Solve the forward problem
[mueller_matrix, mueller_matrix_derivatives] = solve_forward_problem(project_file, wavelengths, material, objective_keys);
% Create a new observation
observation = study.new_observation();
% Add the Mueller matrix
flat_mueller_matrix = flatten_C_style(mueller_matrix);
observation.add(flat_mueller_matrix');
% Add derivatives if available
if objective_keys.derivative_order > 0
for p = 1:length(optimization_domain)
parameter = optimization_domain(p);
if strcmp(parameter.type, 'continuous')
derivative_value = flatten_C_style(mueller_matrix_derivatives.(parameter.name));
observation.add(derivative_value', parameter.name);
end
end
end
end
|
83 84 85 86 87 88 | % Run the minimization
while(not(study.is_done))
sug = study.get_suggestion();
obs = objective(sug.sample);
study.add_observation(obs, sug.id);
end
|
This particular reconstruction can typically be performed in very few iterations despite containing four different parameters, each with a flat prior.

The parameter reconstruction reaches 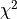 values close to 1 after only a few iterations.¶
values close to 1 after only a few iterations.¶
After 20 iterations the Mueller matrix values have been sufficiently reconstructed.

After 20 iterations the reconstructed Mueller matrix entries are indistinguishable from the target vector.¶