Thin Film Solar Cell¶
Thin-film silicon solar cells rely on scattering structures diffracting incoming light into larger angles thus trapping the light by total internal reflection in the high-index absorber material. Their optimization is a topic of current research. In general the cell is modeled by applying periodic boundary conditions even if the scattering structures are statistical in nature as showcased in this example. This modelling choice accounts for light scattered out of the sides of the unit cell while possibly introducing periodification artifacts. This example relies heavily on the scripting interface describe in Matlab Interface.
This example features a model solar cell with a glass half-space from which the light is incident and a mirror boundary condition on top. A layer with the properties of a transparent conductive oxide (TCO) and an absorber layer mimicking silicon complete the layered solar cell geometry shown in the following.
Geometry Definition and Meshing for a Simple, Random Textured Thin-Film Solar Cell

Left: Geometry and layer designations. Center: Mesh adapted to a short wavelength. Right: Mesh adapted to a long wavelength.¶
The geometry is defined in the template file data_analysis/layout.simple_setup.jcmt. It relies on the input defined in the script data_analysis/run_wavelength_scan.m. The following section of data_analysis/run_wavelength_scan.m loads the random interface defined as x-y-pairs in data_analysis/interface.txt and sets most of the parameters required, such at the thicknesses of the TCO and absorber layers.
%% Setup solar cell geometry
% load interface and shift to zero integral to keep material volume
% constant
interface = load('interface.txt'); % simple list of x y pairs in keys.uol scaling
keys.pitch = diff(interface([1 end],1));
shift = trapz(interface(:,1),interface(:,2))/diff((interface([1 end],1)));
interface(:,2) = interface(:,2)-shift;
interface(:,1) = interface(:,1) - interface(1,1) - keys.pitch/2;
keys.interface = interface.';
keys.thicknesses = [ 600 ;... % tco thickness
300 ]; % silicon thickness
keys.h_offset = max(abs(interface(:,2)))+100;
These parameters are further processed in the scripting section at the beginning of data_analysis/layout.simple_setup.jcmt. Here the appropriate key-value pairs are set up to be used throughout the template.
The cell geometry is built from three polygons: The computational domain, the TCO domain and the silicon domain. The computational domain is defined as a rectangular polygon.
# Computational Domain
Polygon {
Name = "ComputationalDomain"
Points = %(currPoints)e
DomainId = 1
Priority = -1
Boundary {
Number = 1
Class = Transparent
ExteriorDomainId=1
}
Boundary {
Number = 2
Class = Periodic
}
Boundary {
Number = 3
Class = DomainBoundary
BoundaryId=1
}
Boundary {
Number = 4
Class = Periodic
}
For this polygon DomainId = 1 and Priority = ComputationalDomain are used. The specific value of Priority = ComputationalDomain specifies that domain has a smaller priority than all overlapping objects. However, all parts of objects outside of the boundaries of this object are cut off / clipped. Furthermore, all boundary conditions specified on this boundary are inherited by overlapping objects with a higher priority. In this case we assign a Class = Transparent boundary to the first Boundary which are numbered counter clock-wise. The second and fourth boundary segments are set to Class = Periodic. At the top of the model, a perfect electric conductor is assumed, i.e. a perfect loss-less mirror. This is modeled by a Class = Domain boundary condition which is addressed by the specific BoundaryId = 1. The further modelling of this boundary condition is explained in the section Boundary Conditions.
The remaining two polygons are built through a loop in the scripting block in data_analysis/layout.simple_setup.jcmt. The Name, Priority, and DomainId are simple to determine. The TCO layer, like the computational domain, is constructed as a simple quadrilateral whereas the silicon layer includes the textured interface which requires a little more work to account for the thickness offsets of the previous layers.
# Layer Stack
<?
for layer=2:3
keys.mat_name=sprintf('Material_%d',layer);
keys.mat_id = layer;
keys.slc = .5*min(max(real(keys.vacuum_wavelength/keys.uol/keys.n(layer)),100),real(keys.vacuum_wavelength/keys.uol/keys.n(layer)));
if layer>2
dummy = keys.interface;
dummy(2,:)=dummy(2,:)+offsets(layer);
dummy(:,end+(1:2)) = [xLimits(2) xLimits(1); ymax ymax];
keys.currPoints = dummy(:);
else
keys.currPoints = [ xLimits(1) offsets(layer) xLimits(2) offsets(layer) xLimits(2) ymax xLimits(1) ymax];
end
?>
Polygon {
Name = "%(mat_name)s"
Points = %(currPoints)e
DomainId = %(mat_id)d
Priority = %(mat_id)d
MeshOptions{
MaximumSideLength = %(slc)2e
}
Note that we have adapted the mesh options for all domains to respect the wavelength as well as the material properties. This is done to resolve the wave phenomena accurately enough for the derived post processing quantities to remain meaningful.
Boundary Conditions
The cell modeling involves three types of boundary conditions available for electromagnetic modeling in JCMsuite. Here a Transparent boundary is used at the bottom modelling an infinite glass half space. The cell is set up to be a unit cell of an infinitely periodic array in X direction. At the top of the model, a perfect electric conductor is assumed, i.e. a perfect loss-less mirror. In the Layout2D definition above these boundary conditions have already been assigned to the geometry. In case of the Transparent and Periodic setting this does not require any extra work. To model the perfect electric conductor correctly, further definitions are required. These are set in the data_analysis/boundary_conditions.jcm and the data_analysis/sources.jcmt files.
In boundary_conditions.jcm a BoundaryCondition is defined. On the specified BoundaryId the electromagnetic field is set to include only a TangentialElectric component.
BoundaryCondition {
BoundaryId = 1
Electromagnetic = TangentialElectric
}
In sources.jcmt the source definition must then include a value for the ElectricFieldStrength at the boundary. This is set to [0.0 0.0 0.0].
Source {
BoundaryId = 1
ElectricFieldStrength = [0.0 0.0 0.0]
}
Note
In case multiple SourceBags are used, sources at the boundaries must be defined in every SourceBag.
Source Definition
The illumination in this example is modeled as a z-polarized plane wave incident from the lower half space. This is considered a good enough approximation to solar illumination on earth at the length scales involved. As the illumination wavelength is parameterized, the template contains a scripting section which sets the appropriate keys for the k-vector K and the Amplitude. Note that in this a more simple definition of the PlaneWave source is also possible. For details see Plane Wave
The special setting of a perfect electric conductor in this example requires additional care of the Source definition. As described in the section Boundary Conditions an additional Source on the boundary must be defined. Furthermore, this step necessitates the declaration of the source domain identified by DomainId = 1 which for problems without DomainBoundaries the solver is able to determine automatically.
<?
keys.k_vector = 2*pi/keys.vacuum_wavelength*real(keys.n(1))*[0 1 0];
keys.U_s = [0 0 1];
?>
SourceBag {
Source {
DomainId = 1
ElectricFieldStrength {
PlaneWave {
K = %(k_vector)e
Amplitude = %(U_s)e
}
}
}
Source {
BoundaryId = 1
ElectricFieldStrength = [0.0 0.0 0.0]
}
}
Material Definition
The material properties have crucial influence on the results of the simulation. There are many different material databases available on the internet and in the literature. In this example we employ the freely available data sets from http://www.refractiveindex.info/ for the silicon material data. For glass we assume a constant refractive index of 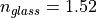 and for the TCO we assume
and for the TCO we assume 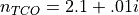 . These are initialized in the
. These are initialized in the run_wavelength_scan.m script.
% refractive indices
keys.n(1) = 1.52; % glass
keys.n(2) = 2.1+.01*1i; % tco
keys.n(3) = 1; % silicon
To account for the dispersive nature of the material parameters, the material data is interpolated for the corresponding wavelength in the run_wavelength_scan.m script. It is imported into Matlab??
% load material data for Si from file
Si = importdata('Si.txt',' ', 13); Si = Si.data;
Si(:,1) = Si(:,1)*1e-9; [foo,I] = unique(Si(:,1)); Si = Si(I,:);
and later interpolated for the corresponding wavelength.
keys.n(3) = interp1(Si(:,1), Si(:,2), keys.vacuum_wavelength, 'linear') ... % n
+ 1i*interp1(Si(:,1), Si(:,3), keys.vacuum_wavelength, 'linear'); % k
Note
A linear interpolation might not be a good choice, e.g. for coarse data sets with exponentially decaying imaginary parts of the refractive index. Here, a linear interpolation might overestimate absorption.
The template materials.jcmt contains a very simple loop over all materials in which a Name is derived from the Id and the RelPermittivity is computed from the refractive indices set in the script run_wavelength_scan.m.
<?
for mat = 1:length(keys.n)
keys.permittivity = (keys.n(mat))^2;
keys.mat_id=mat;
keys.mat_name = sprintf('Material_%d', mat);
?>
Material {
Name = "%(mat_name)s"
DomainId = %(mat_id)e
RelPermittivity = %(permittivity)e
RelPermeability = 1.0
}
<?
end
?>
Project Setting
The project.jcmpt files contains the solver settings required to solve the previously set up model. It is solved as a time-harmonic electromagnetic scattering problem.
Project {
InfoLevel = 3
Electromagnetics {
TimeHarmonic {
Scattering {
Accuracy {
FiniteElementDegree = %(fe_degree)i
Precision = %(precision)e
Refinement {
MaxNumberSteps = %(n_refinement_steps)i
PreRefinements = %(n_prerefinement_steps)i
}
}
}
}
}
}
To steer Accuracy several settings are made in run_wavelength_scan.m. A Precision of 0.01 and a FiniteElementDegree = 2 is used. One adaptive refinement step is taken and assures a reasonably accurate simulation result.
% solver settings
keys.n_refinement_steps = 1;
keys.n_prerefinement_steps = 0;
keys.precision = 1e-2;
keys.fe_degree = 2;
Post Processing
The post processing steps required to compute absorption and reflection of the solar cell model are defined in project.jcmp. The absorption can be derived from either the DensityIntegration PostProcess or the FluxIntegration PostProcess. The DensityIntegration PostProcess integrates the ElectromagneticFieldAbsorption quantity. This gives rise to the power loss within the absorber layer due to an imaginary part of the permittivity. As the glass block is assumed to be transparent, it would be sufficient to restrict the computation to DomainIds = [2,3].
PostProcess {
DensityIntegration {
FieldBagPath = "./project_results/fieldbag.jcm"
OutputFileName = "./project_results/field_energy.jcm"
OutputQuantity = ElectromagneticFieldAbsorption
}
}
Alternatively, the absorption can also be computed by looking at the net fluxes of the ElectromagneticFieldEnergyFlux across domain boundaries. This also allows to compute the reflected flux leaving the computational domain.
PostProcess {
FluxIntegration {
InterfaceType = DomainInterfaces
FieldBagPath = "./project_results/fieldbag.jcm"
OutputFileName = "./project_results/energy_flux.jcm"
OutputQuantity = ElectromagneticFieldEnergyFlux
}
}
The Fourier Transform of the outgoing electromagnetic field allows for a more detailed account of the direction of the scattered light. It is also included in the project.jcmpt file.
PostProcess {
FourierTransform {
FieldBagPath = "./project_results/fieldbag.jcm"
OutputFileName = "./project_results/propagating_fourier_coefficients_down.jcm"
NormalDirection = -Y
}
}
Simulation Run
The script data_analysis/run_wavelength_scan.m sets up the simulation and executes the wavelength scan. Excerpts have already been discussed in the sections above. The central part of the script is the following loop over the different wavelengths.
for ii = 1:length(wavelengths)
keys.vacuum_wavelength = wavelengths(ii)*keys.uol;
keys.n(3) = interp1(Si(:,1), Si(:,2), keys.vacuum_wavelength, 'linear') ... % n
+ 1i*interp1(Si(:,1), Si(:,3), keys.vacuum_wavelength, 'linear'); % k
%% Solve
results = jcmwave_solve('--solve', 'project.jcmp', keys,'jcmt_pattern','simple_setup');
%% Absorbed energy
absorption(:,ii) = results{2}.ElectromagneticFieldAbsorption{1}/p_in;
%% Fourier Transform
e_field = cell2mat(results{3}.ElectricFieldStrength);
km = norm(results{3}.K(ceil(end/2),:));
angles = real(acosd(-results{3}.K(:,2)/km));
refl = sum(conj(e_field).*e_field,2).'*cosd(angles);
reflection(ii) = sum(refl,1)*.5/Z0*keys.n(1)*keys.pitch*keys.uol/p_in;
%% Flux outgoing
energy_flux = cell2mat(results{4}.ElectromagneticFieldEnergyFlux);
index = results{4}.DomainIdFirst == 2 & results{4}.DomainIdSecond == 3;
absorption_via_flux(ii) = real(energy_flux(index))/p_in;
index = results{4}.DomainIdFirst == 2 & results{4}.DomainIdSecond == 1;
reflection_via_flux(ii) = real(p_in+energy_flux(index))/p_in;
%% Statistics
total_time(ii) = results{1}.computational_costs.TotalTime(end);
unknowns(ii) = results{1}.computational_costs.Unknowns(end);
mem(ii) = results{1}.computational_costs.TotalMemory_GB(end);
end
Within this loop the variable keys.vacuum_wavelength is set to the correct value and the interpolation of the material data is executed. Subsequently the project is solved by the appropriate call to jcmwave_solve with the keys structure and the jcmt_pattern as additional arguments.
The obtained results from the post processes are returned in the cell array results in the order defined in data_analysis/project.jcmpt. A scaling with  of the electromagnetic field absorption in the absorbing layers gives rise to the absorbed fraction of incident power to the domain.
of the electromagnetic field absorption in the absorbing layers gives rise to the absorbed fraction of incident power to the domain.
In similar ways, the output of the FluxIntegration and FourierTransform are processed and scaled to obtain the reflected and absorbed fractions of the incident power.
Finally the simulated results are plotted as implied EQE and 1-reflection over wavelength and as an area plot with absorptance in the difference cell layers as well as reflections. The sampling_rate variable allows to refine the sampling rate of the wavelength_interval.
The final section of the script executes the weighting with the AM1.5 solar spectrum to compute implied photo current densities. To compute this, the spectrum is first loaded from a csv file data_analysis/ASTMG173.csv which is a slightly reformatted version of the file ASTMG173.xls available at http://rredc.nrel.gov/solar/spectra/am1.5/. From the data in this file the photon count per second is computed and the spectral_weight determined at the simulated wavelengths. Numerical integration and scaling with the elementary charge allows to display the simulated implied photo current densities for the silicon absorber as well as the parasitic losses in the TCO and the reflection losses.
%% Solar Spectrum
solar_spectrum_data = importdata('ASTMG173.csv',';',2); % Data is reformatted from ASTMG173.xls available at http://rredc.nrel.gov/solar/spectra/am1.5/
planck = 6.62606957*10^-34; % Planck's constant
energy = planck*c0/keys.uol./solar_spectrum_data.data(:,1); % photo energy
photon_number = solar_spectrum_data.data(:,3)./energy*1e-4; % number of photons in cm-2 nm^-1 s-1
spectrum_weight = interp1(solar_spectrum_data.data(:,1),photon_number,wavelengths);
eC = 1.602176565*10^-19; % elementary charge
currentDensity = eC*trapz(wavelengths,[absorption.*repmat(spectrum_weight,3,1)]')*1000;
currentDensity(3) = eC*trapz(wavelengths,reflection.*spectrum_weight)*1000;
fprintf('\n Implied photo current densities in (%dnm, %dnm):\n %g mAcm-2 (TCO)\n %g mAcm-2 (Si)\n %g mAcm-2(R)\n\n',round(wavelengths([1 end])), currentDensity)
