Rib Waveguide¶
This tutorial example demonstrates mode analysis for a typical rib waveguide of an integrated photonic circuit:
Depending on the design and functionality of the integrated circuit, such waveguides appear as straight or curved structures. JCMsuite allows convenient analysis of straight and bended cases. The geometrical setup defines the cross section of the waveguide:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | Layout2D {
Name = "Rib Waveguide"
UnitOfLength = 1e-06
MeshOptions {
MaximumSideLength = 0.5
}
Objects {
Parallelogram {
Name = "ComputationalDomain"
Width = 3
Height = 3
DomainId = 1
Priority = ComputationalDomain
Boundary {
Class = Transparent
}
}
Parallelogram {
Name = "Substrate"
Width = 3
Height = 1
DomainId = 3
GlobalPosition = [0 -1]
}
Parallelogram {
Name = "Waveguide"
Width = 0.3
Height = 1
DomainId = 2
}
}
}
|
In the project file the numerical propagating mode setup is defined:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | Project {
InfoLevel = 3
Electromagnetics {
TimeHarmonic {
PropagatingMode {
AxisPositionX = -1e-6
Lambda0 = 1.5e-6
Accuracy {
Precision=1e-6
Refinement {
PreRefinements = 2
MaxNumberSteps = 1
}
}
SelectionCriterion {
NearGuess {
Guess = 3.0
NumberEigenvalues = 1
}
}
}
}
}
}
|
Here, the parameter AxisPositionX = -1e-6 is used to set the curvature of the waveguide problem. Thereby, the 2D cross section is treated as if it would be swept along a circle around the 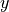 -axis. The
-axis. The 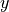 -axis is displaced additionally by
-axis is displaced additionally by AxisPositionX, i.e. the 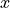 -position of the cylindrical axis is located at
-position of the cylindrical axis is located at AxisPositionX. The case AxisPositionX -> -Infinity converges to the unbended/straight case, which is active, when parameter AxisPositionX is omitted. The computed effective refractive index for 1e-6 radius of curvature is 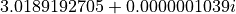 . Compared to the straight case, which gives an effective refractive index of
. Compared to the straight case, which gives an effective refractive index of 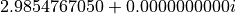 , the imaginary part of the effective refractive index quantifies radiation losses due to leakage of the mode when traveling along the curved waveguide.
, the imaginary part of the effective refractive index quantifies radiation losses due to leakage of the mode when traveling along the curved waveguide.
Below the intensity and vector field of the fundamental mode is shown for the curved waveguide:


