Plasmonic Waveguide¶
This example demonstrates computation of a plasmon-polariton wave guided by a thin silver film that is bounded by different dielectrics. The setup follows an example from Berini [1]. We comment mainly on the numerical solution for the electric field intensity on the whole computational domain, which represents a plasmon-polariton. However, for propagation mode projects also the propagation constant (Propagating Mode) is computed.
The geometry is sketched in the following figure:

The relative permittivities of the lower and upper materials are given by 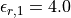 and
and  . The metal film has a thickness of
. The metal film has a thickness of 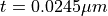 and a width of
and a width of  . The structure is analyzed for a vacuum wavelength
. The structure is analyzed for a vacuum wavelength 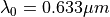 . The metal film (silver) has a relative permittivity of
. The metal film (silver) has a relative permittivity of 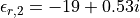 at this wavelength.
at this wavelength.
In this example we compute the 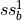 -mode which has a mirror symmetric electric field with respect to the symmetry plane of the waveguide [1].
Therefore it suffices to discretize only one half of the geometry. In the layout file the symmetry plane is attributed with
-mode which has a mirror symmetric electric field with respect to the symmetry plane of the waveguide [1].
Therefore it suffices to discretize only one half of the geometry. In the layout file the symmetry plane is attributed with BoundaryClass=Mirror. The symmetry type of the desired propagation mode is specified within the project file:
Project {
Electromagnetics {
TimeHarmonic {
PropagatingMode {
FieldComponents = ElectricXYZ
MirrorSymmetry=Symmetric
}
}
}
}
At the outer boundaries of the computational domain (BoundaryId=1 in the layout file) we assume that the tangential component of the electric field has decayed to zero so that the boundary_conditions.jcm file reads as
BoundaryCondition {
BoundaryId = 1
Electromagnetic = TangentialElectric
}
At the corners of the metal film singularities are expected, therefore corner refinements of the mesh are defined in the layout file:
Parallelogram {
...
MeshOptions {
CornerRefinement {
MaximumSidelength = 0.001
}
}
Further refinements are done self-adaptively by the solver. In the project file the number of refinement steps can be chosen.
Accuracy {
Precision = 0.01
Refinement {
MaxNumberSteps = 4
PreRefinements = 0
}
}
A section of the triangulated geometry after the last step of refinement is shown in the figure below.

Cutout of the refined mesh. Since mirror symmetry is applied only the right half of the domain is discretized.¶
The accurate computation of plasmon-polariton modes is a challenging problem due to the singular field behaviour near the metal corners and due to the multi-scale structure of the geometry. The propagating plasmon-polariton is mainly located in the vicinity of the very thin silver strip. An adaptive finite element discretization is the method of choice for such problems. Due to corner pre-refinement and to adaptive refinement steps the mesh is refined especially close to the strip and close to the metal corners where the electric field shows singular behavior and where it has to be resolved very accurately. The resulting field is shown in the following figure:
The magnetic field can be easily obtained using the post process ExportField.
PostProcess {
ExportFields {
FieldBagPath = "project_results/fieldbag.jcm"
OutputFileName = "project_results/fieldbag_magnetic.jcm"
OutputQuantity = MagneticFieldStrength
}
}
By default the field is calculated on the original grid.
References
| [1] | (1, 2)
|
